【知识】 扩展欧几里得算法

前言

扩展欧几里得算法是一个常用的数论算法，可以用于求解不定方程、线性同余方程、模意义下的乘法逆元等。网上很多资料对于代码的关键部分证明十分模糊，这篇文章带你完全理解扩展欧几里得算法。

回顾普通欧几里得算法

大部分人初学算法肯定会接触到求最大公约数的欧几里得算法，它也叫做 「辗转相除法」。

它的求解过程十分简单：

int gcd(int a, int b) {
    if (b == 0) return a;         // 余数为 0，除尽了
    else return gcd(b, a % b);    // 大数模去小数，递归计算
}

原理也可以用小学二年级知识理解：假设 （）的最大公因数是一个苹果，则 肯定都是若干个苹果，则 也肯定是若干个苹果，故 和 的最大公因数也是一个苹果，然后按照前面的方法 「辗转相除」，最后 为 时就说明上一步模出来的余数为 ，这时这一步的 （也就是上一步的 ）一个苹果啦。

刚才的过程中我们用到了欧几里得定理，即 ，不过证明过程简化了。

由此我们还可以得出每一层递归时的 都是一样的（废话。

历史资料

欧几里得算法，又称辗转相除法，被认为是世界上最早的算法（公元前 年）。辗转相除法首次出现于欧几里得的 《几何原本》 第 Ⅶ 卷，命题 Ⅰ 和 Ⅱ。

在中国，东汉出现的 《九章算术》 中介绍了一种与欧几里得算法的弱化版 「更相减损法」，其实就是把取模换成了一点一点地减。

扩展欧几里得算法

首先我们需要知道 「裴蜀定理」：对于任意 都存在 满足 （注意这里的 可以为负）。

裴蜀定理的一个推论是，不定方程 若存在合法解，则必定会有 （可以理解为把 都翻了几倍），也就是说 最小为 。

于是我们可以通过这种方法来判断不定方程 是否有解。

但人类仍不知足……我还想知道在 的情况下，解到底是多少（把这个解翻个若干倍就是其他解了，因为 一定是 的倍数。

注意：扩展欧几里得算法算法只能解 的不定方程。

它的实现方法是在普通欧几里得算法递归求 回溯的时候顺带把 算出来（因为要先求 ）。

计算 的过程：我们在回溯到某一层的算出的 都是关于当前层的 满足 （每一层的 都一样）。

详细计算方法请看下面代码详解（保证对每一句话都做详细解释）：

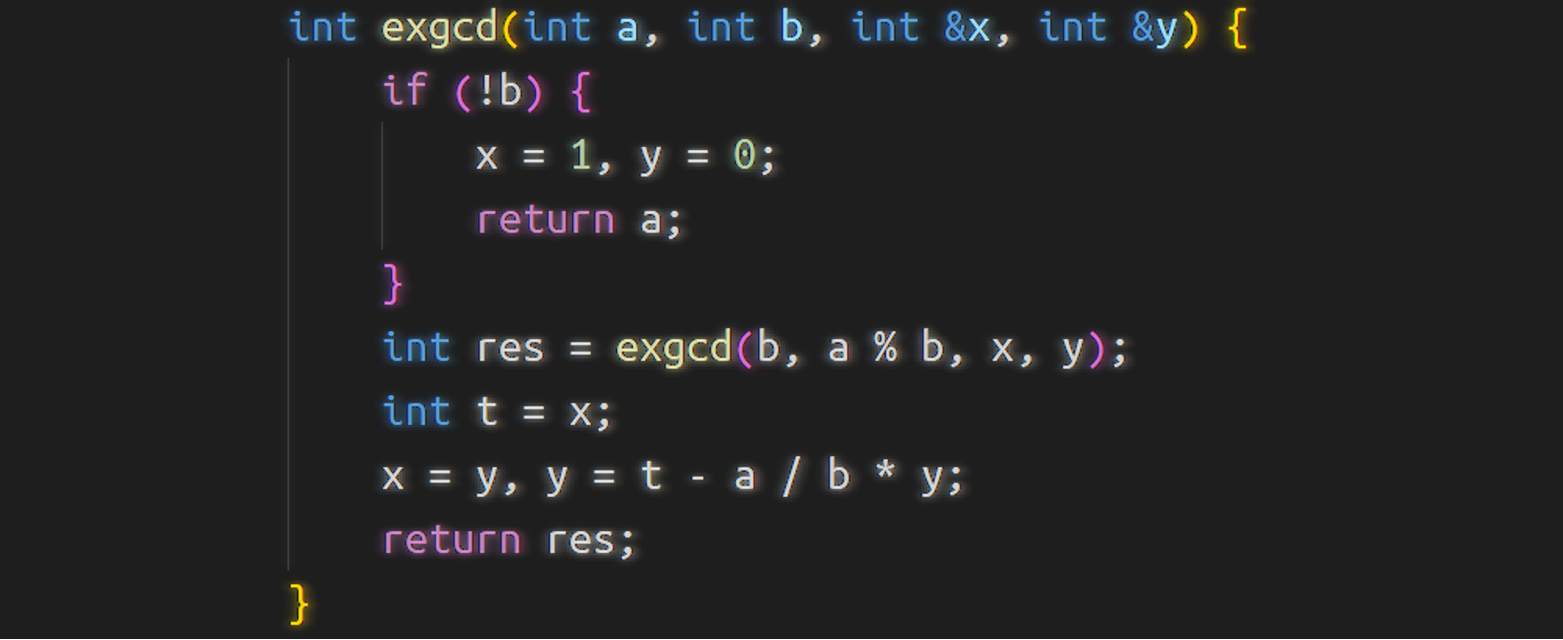
int exgcd(int a, int b, int &x, int &y) {  // 这里x和y都要被修改，所以使用引用参数
    if (!b) {							// b等于0，到达递归出口
        x = 1, y = 0;					// 此时的a为gcd，x=1,y=0可满足条件
        return a;
    }
    int res = exgcd(b, a % b, x, y);	// 存下gcd
    int t = x;							// 将下一层的x暂存下来
    x = y, y = t - a / b * y;			// 这个请看下面解释
    return res;
}

其实我们可以发现，如果我们只要求 的话返回 没有任何用，可以直接写成 void 类型。

对于 x = y, y = t - a / b * y; 这个计算，我第一次看到的时候也觉得十分神秘，为什么这样推出来的 可以满足条件呢？

重点来了！！！接下来的证明网上很多自称 「超详解」 的教程都没讲或糊弄一下就过去了。过程并不复杂，大概只有初中知识，长点脑子的应该都能看懂。

设当前层要求的 分别为 ，下一层已经求好了的 分别为 （回溯时从下往上推）。

则

由欧几里得定理可知：

故

又因为

将其代入 式得

展开得

即

又因为 ，

且注意到 与 对应， 与 对应，

故 。

以上证明过程来自 OI Wiki 扩展欧几里得算法 ，稍有改动。

然后我们的 x = y, y = t - a / b * y; 就出来啦！是不是觉得很神奇！

最后我们要求不定方程 的解时只需要这样调用：

int x, y;					// 因为是引用参数，所以x和y需要单独开变量
int d = gcd(a, b, x, y);	// 此时x和y里就是对应的解，d就是a和b的最大公因数